Solution to Exercise 2.2¶

Learning curves for DDPG in HalfCheetah-v2 for bugged and non-bugged actor-critic implementations, averaged over three random seeds.

You Should Know

This page will give the solution primarily in terms of a detailed analysis of the Tensorflow version of this exercise. However, the problem in the PyTorch version is basically the same and so is its solution.

The Bug in the Code: Tensorflow Version¶

The only difference between the correct actor-critic code,

"""
Actor-Critic
"""
def mlp_actor_critic(x, a, hidden_sizes=(400,300), activation=tf.nn.relu,
                     output_activation=tf.tanh, action_space=None):
    act_dim = a.shape.as_list()[-1]
    act_limit = action_space.high[0]
    with tf.variable_scope('pi'):
        pi = act_limit * mlp(x, list(hidden_sizes)+[act_dim], activation, output_activation)
    with tf.variable_scope('q'):
        q = tf.squeeze(mlp(tf.concat([x,a], axis=-1), list(hidden_sizes)+[1], activation, None), axis=1)
    with tf.variable_scope('q', reuse=True):
        q_pi = tf.squeeze(mlp(tf.concat([x,pi], axis=-1), list(hidden_sizes)+[1], activation, None), axis=1)
    return pi, q, q_pi

and the bugged actor-critic code,

"""
Bugged Actor-Critic
"""
def bugged_mlp_actor_critic(x, a, hidden_sizes=(400,300), activation=tf.nn.relu,
                            output_activation=tf.tanh, action_space=None):
    act_dim = a.shape.as_list()[-1]
    act_limit = action_space.high[0]
    with tf.variable_scope('pi'):
        pi = act_limit * mlp(x, list(hidden_sizes)+[act_dim], activation, output_activation)
    with tf.variable_scope('q'):
        q = mlp(tf.concat([x,a], axis=-1), list(hidden_sizes)+[1], activation, None)
    with tf.variable_scope('q', reuse=True):
        q_pi = mlp(tf.concat([x,pi], axis=-1), list(hidden_sizes)+[1], activation, None)
    return pi, q, q_pi

is the tensor shape for the Q-functions. The correct version squeezes ouputs so that they have shape [batch size], whereas the bugged version doesn’t, resulting in Q-functions with shape [batch size, 1].

The Bug in the Code: PyTorch Version¶

In the PyTorch version of the exercise, the difference is virtually the same. The correct actor-critic code computes a forward pass on the Q-function that squeezes its output:

"""
Correct Q-Function
"""
class MLPQFunction(nn.Module):

    def __init__(self, obs_dim, act_dim, hidden_sizes, activation):
        super().__init__()
        self.q = mlp([obs_dim + act_dim] + list(hidden_sizes) + [1], activation)

    def forward(self, obs, act):
        q = self.q(torch.cat([obs, act], dim=-1))
        return torch.squeeze(q, -1) # Critical to ensure q has right shape.

while the bugged version does not:

"""
Bugged Q-Function
"""
class BuggedMLPQFunction(nn.Module):

    def __init__(self, obs_dim, act_dim, hidden_sizes, activation):
        super().__init__()
        self.q = mlp([obs_dim + act_dim] + list(hidden_sizes) + [1], activation)

    def forward(self, obs, act):
        return self.q(torch.cat([obs, act], dim=-1))

How it Gums Up the Works: Tensorflow Version¶

Consider the excerpt from the part in the code that builds the DDPG computation graph:

# Bellman backup for Q function
backup = tf.stop_gradient(r_ph + gamma*(1-d_ph)*q_pi_targ)

# DDPG losses
pi_loss = -tf.reduce_mean(q_pi)
q_loss = tf.reduce_mean((q-backup)**2)

This is where the tensor shape issue comes into play. It’s important to know that r_ph and d_ph have shape [batch size].

The line that produces the Bellman backup was written with the assumption that it would add together tensors with the same shape. However, this line can also add together tensors with different shapes, as long as they’re broadcast-compatible.

Tensors with shapes [batch size] and [batch size, 1] are broadcast compatible, but the behavior is not actually what you might expect! Check out this example:

>>> import tensorflow as tf
>>> import numpy as np
>>> x = tf.constant(np.arange(5))
>>> y = tf.constant(np.arange(5).reshape(-1,1))
>>> z1 = x * y
>>> z2 = x + y
>>> z3 = x + z1
>>> x.shape
TensorShape([Dimension(5)])
>>> y.shape
TensorShape([Dimension(5), Dimension(1)])
>>> z1.shape
TensorShape([Dimension(5), Dimension(5)])
>>> z2.shape
TensorShape([Dimension(5), Dimension(5)])
>>> sess = tf.InteractiveSession()
>>> sess.run(z1)
array([[ 0,  0,  0,  0,  0],
       [ 0,  1,  2,  3,  4],
       [ 0,  2,  4,  6,  8],
       [ 0,  3,  6,  9, 12],
       [ 0,  4,  8, 12, 16]])
>>> sess.run(z2)
array([[0, 1, 2, 3, 4],
       [1, 2, 3, 4, 5],
       [2, 3, 4, 5, 6],
       [3, 4, 5, 6, 7],
       [4, 5, 6, 7, 8]])
>>> sess.run(z3)
array([[ 0,  1,  2,  3,  4],
       [ 0,  2,  4,  6,  8],
       [ 0,  3,  6,  9, 12],
       [ 0,  4,  8, 12, 16],
       [ 0,  5, 10, 15, 20]])

Adding or multiplying a shape [5] tensor by a shape [5,1] tensor returns a shape [5,5] tensor!

When you don’t squeeze the Q-functions, q_pi_targ has shape [batch size, 1], and the backup—and in turn, the whole Q-loss—gets totally messed up.

Broadcast error 1: (1 - d_ph) * q_pi_targ becomes a [batch size, batch size] tensor containing the outer product of the mask with the target network Q-values.

Broadcast error 2: r_ph then gets treated as a row vector and added to each row of (1 - d_ph) * q_pi_targ separately.

Broadcast error 3: q_loss depends on q - backup, which involves another bad broadcast between q (shape [batch size, 1]) and backup (shape [batch size, batch size]).

To put it mathematically: let $q$ , $q'$ , $r$ , $d$ denote vectors containing the q-values, target q-values, rewards, and dones for a given batch, where there are $n$ entries in the batch. The correct backup is

$z_i = r_i + \gamma (1-d_i) q'_i,$

and the correct loss function is

$\frac{1}{n} \sum_{i=1}^n (q_i - z_i)^2.$

But with these errors, what gets computed is a backup matrix,

$z_{ij} = r_j + \gamma (1-d_j) q'_i,$

and a messed up loss function

$\frac{1}{n^2} \sum_{i=1}^n \sum_{j=1}^n (q_j - z_{ij})^2.$

If you leave this to run in HalfCheetah long enough, you’ll actually see some non-trivial learning process, because weird details specific to this environment partly cancel out the errors. But almost everywhere else, it fails completely.

How it Gums Up the Works: PyTorch Version¶

Exactly the same broadcasting shenanigans as in the Tensorflow version. Check out this note in the PyTorch documentation about it.

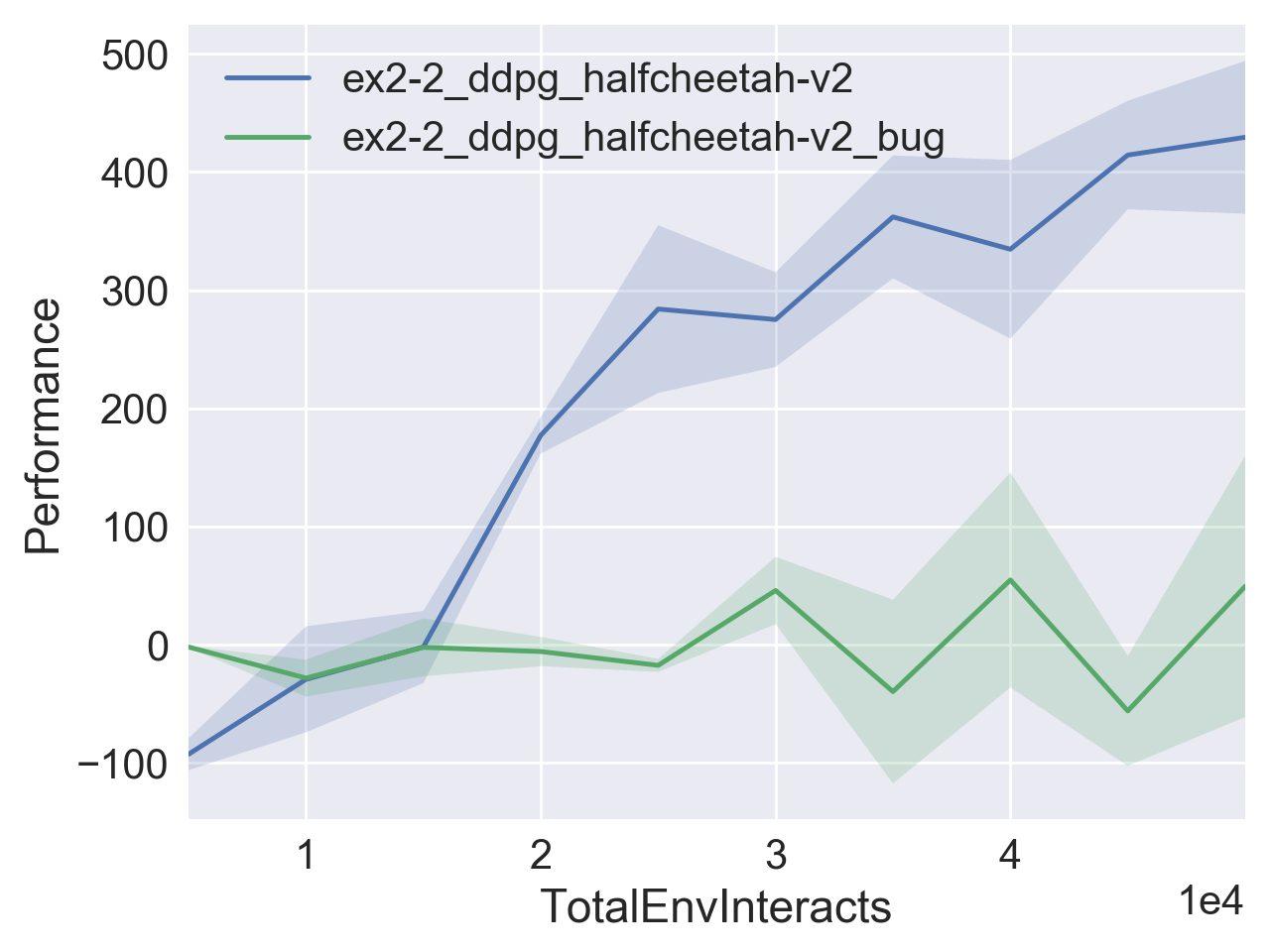
Learning curves for DDPG in HalfCheetah-v2 for bugged and non-bugged actor-critic implementations using PyTorch, averaged over three random seeds.